Calculer un escalier quart tournant
1 - Introduction
Cette article est la suite de celui traitant de l’escalier droit. Il est donc préférable de l’avoir lu avant de se lancer dans celui-ci.
Le calcul de l’escalier à quart tournant n’a pas de grande différence avec l’escalier droit. Le palier n’étant qu’une marche dont le giron a été augmenté suffisamment pour pouvoir y stationner.
Pour la conception, deux point sont important à anticiper :
- La continuité des limons au niveau du palier intermédiaire
- La continuité de la rampe
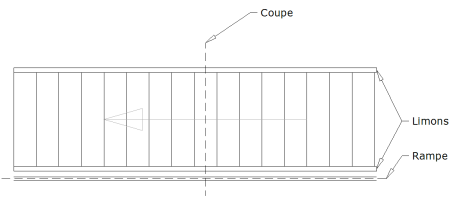
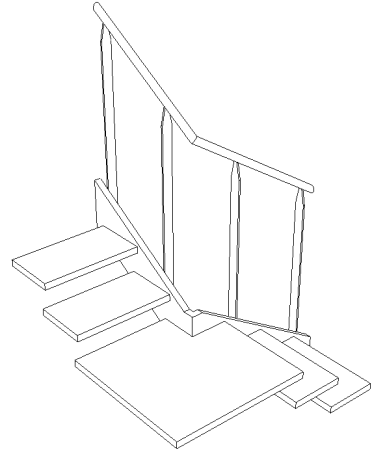
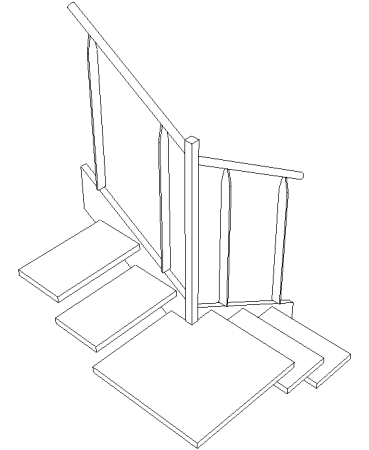
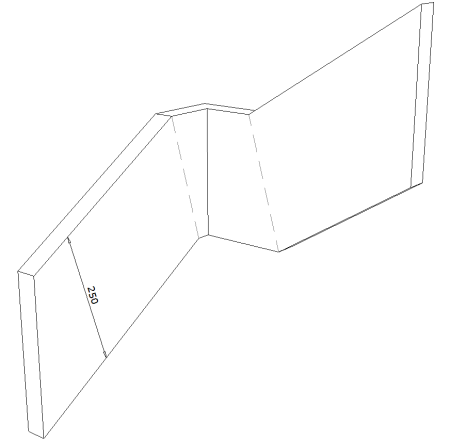
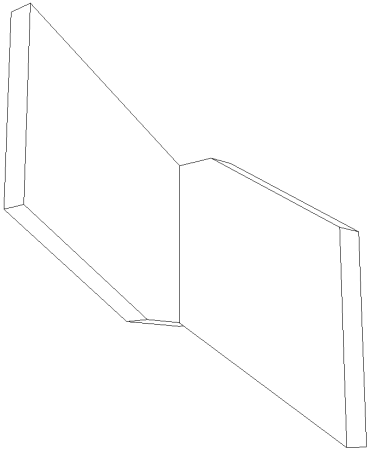
Un exemple pour bien comprendre le problème :
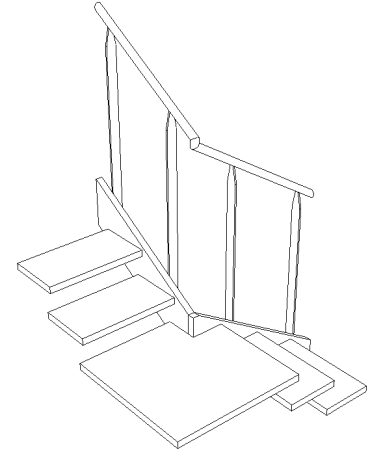
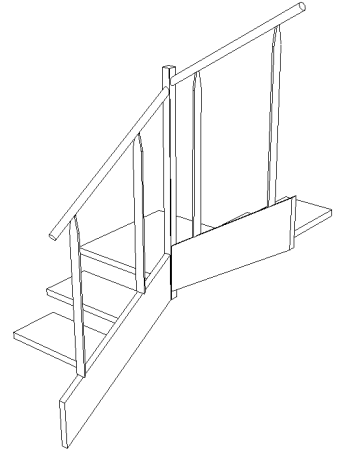
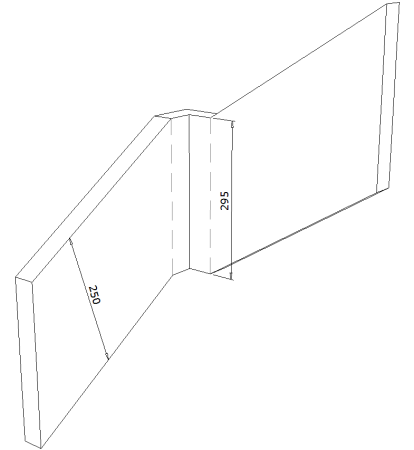
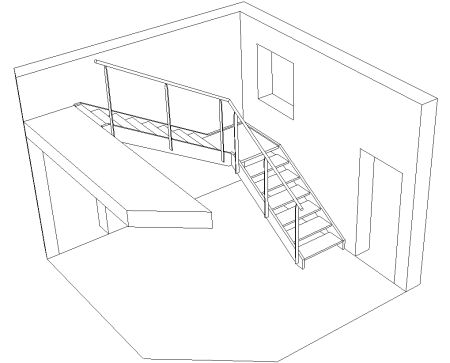
Quand ces deux points sont respectés, c’est plus joli :
2 - Le principe
Le calcul d’un escalier quart tournant s’effectue de la même façon qu’un escalier droit. Il faudra simplement couper l’escalier droit en deux pour obtenir le quart tournant.
Un escalier droit :
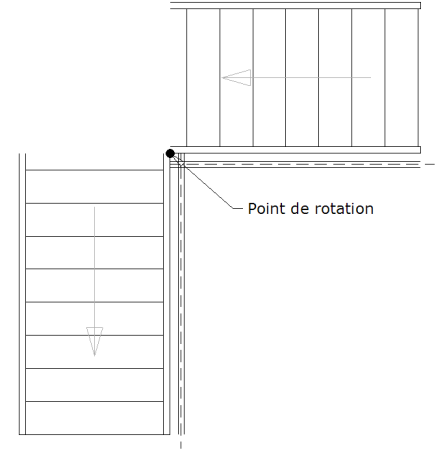
On coupe sur les pointillés et on tourne de 90° :
On ajuste les limons et la rampe :
Suivant le point de rotation utilisé, la continuité de la rampe et du limon sera plus ou moins respectée.
Pour cet exemple j’ai positionné arbitrairement le point de rotation sur la face extérieur du limon.
3 - Positions du point de rotation
Voici trois situations avec leurs avantages et inconvénients suivant la position du point de rotation.
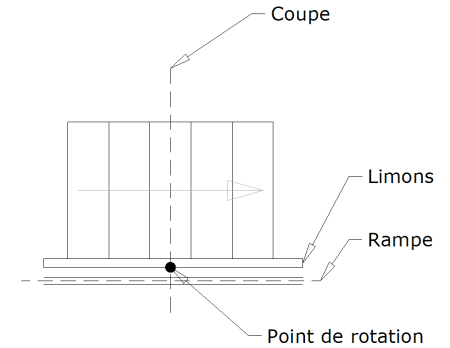
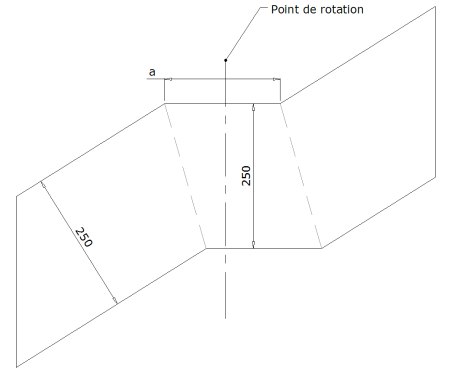
3.1 - Sur la face intérieur du limon :
En plan :
En perspective :
Avantage :
- Encombrement minimum du palier
Inconvénients :
- Limon et main courante mal raccordés
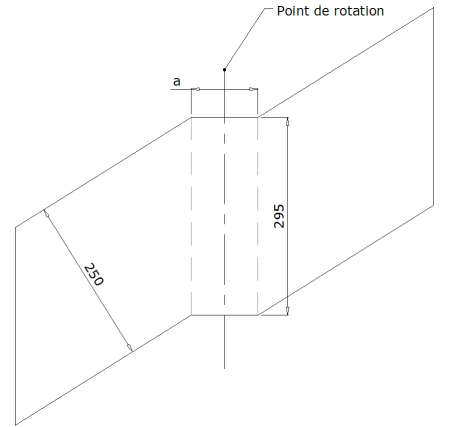
3.2 - Sur la face extérieur du limon :
En plan :
En perspective :
Avantage :
- Limon correctement raccordée
Inconvénients :
- Main courante mal raccordés
- Palier un peu plus encombrant que la situation précédente
3.3 - Sur l’axe de la main courante :
En plan :
En perspective :
Avantage :
- Limon et main courante correctement raccordés
Inconvénients :
- Encombrement maximum du palier
3.4 - Conclusion
Je trouve cette dernière solution la plus jolie mais suivant la place disponible, il faudra choisir entre l’esthétique et le pratique.
Il faut également savoir que plus le point de rotation s’éloignera de la ligne de foulée, plus l’angle de l’escalier augmentera.
Pour éviter des raccords trop compliqué, cette situation peut être également envisagée :
Un tube carré est placé à l’intersection des deux limons. Il n’y a pas de raccord directe entre les main courantes et les limons. Cela peut être un bon compromis entre esthétique et encombrement
En plan :
En perspective :
4 - En pratique
Il y a plusieurs façon d’aborder le problème suivant les contraintes de site.
Comme je l’ai montré plus haut, un escalier quart tournant peut être considéré comme un escalier droit coupé en deux.
Cette méthode a deux avantages :
- Elle permet d’avoir des girons et des hauteurs constant sur tout l’escalier et donc facilite la fabrication.
- La continuité des raccords de main courante et de limon peuvent être facilement anticipé.
Par contre, elle ne laisse pas la possibilité de positionner le palier à une hauteur donnée. Et dans certain cas, on ne peut pas faire autrement.
La 2ème solution, aborde le problème en considérant l’escalier quart tournant comme une succession d’escaliers droit séparés pas des paliers. Chaque escalier est donc indépendant.
Dans ce cas, on peut positionner le palier puis calculer les escaliers s’y rapportant. Mais contrairement à la solution précédente, les girons et les hauteurs ne seront pas constant. Au maximum, on peut obtenir des hauteurs constantes en positionnant le palier sur une division commune de la hauteur à gravir pour les deux volées.
Cette solution empêche également de conserver la continuité des raccords de rampe et de limon.
Je ne vous présenterais donc que la première méthode, la second se résumant au calcul de deux escalier droit.
4.1 - Exemple
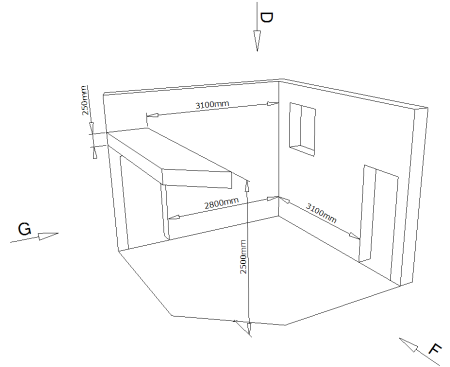
La prise de cote s’effectue de la même façon que pour l’escalier droit.
4.1.1 - Les étapes de calcul :
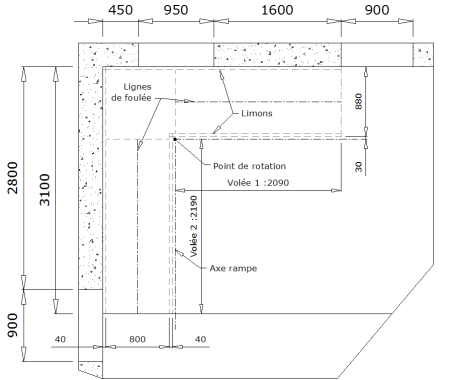
4.1.1.1 - Implanter l’escalier
sur la vue de dessus avec les limons et l’axe de la main courante.
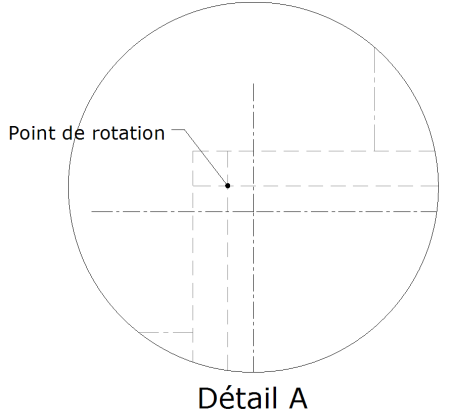
4.1.1.2 - Positionner le point de rotation
en fonction du résultat souhaité, (voir chapitre précédent) ici le point de rotation se situe sur la rampe et en déduire la longueur des volées
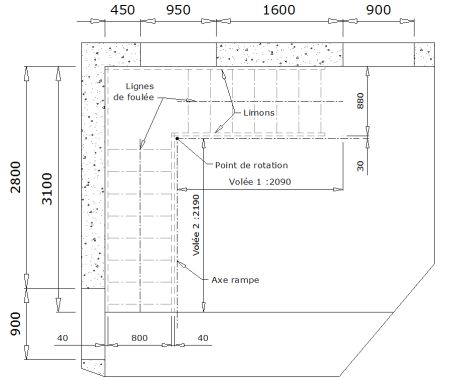
4.1.1.3 - Effectuer une rotation de 90°
autour du point de rotation pour obtenir un escalier droit
4.1.1.4 - Calculer l’escalier comme un escalier droit
sans oublier la marche palière (voir l’article sur l’escalier droit)
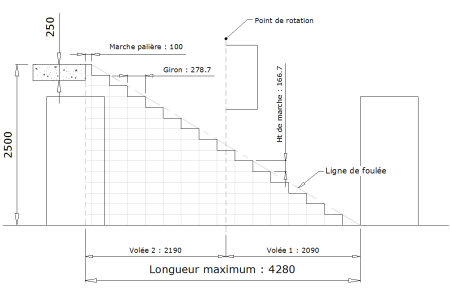
Pour cet exemple, on prendra en compte une marche palière de 100mm. La deuxième volée sera plus courte de 100mm.
- Diviser la hauteur de l’escalier (2500) par une hauteur moyenne de 175mm :
- 2500 ÷ 175 = 14.3 ==> Nombre de divisions possibles
- 2500 ÷ 14 = 178,6 ==> Hauteur de marche avec 14 divisions
- 2500 ÷ 15 = 166,7 ==> Hauteur de marche avec 15 divisions
- Diviser la longueur maximum moins la marche palière (4280 - 100 = 4180) par le nombre de divisions trouvé (14 et 15) :
- 4180 ÷ 14 = 298,6 ==> Giron avec 14 divisions
- 4180 ÷ 15 = 278,7 ==> Giron avec 15 divisions
- Vérification de la formule de Blondel :
[Rappel : 2 × hauteur de marche + 1 × giron = 630]- En utilisant 14 divisions : 178,6 × 2 + 298,6 = 656
- En utilisant 15 divisions : 166,7 × 2 + 278,7 = 612
Le cas avec 15 division se rapproche le plus de 630 :
- 15 divisions
- Hauteur de marche : 166,7
- Giron : 278,7
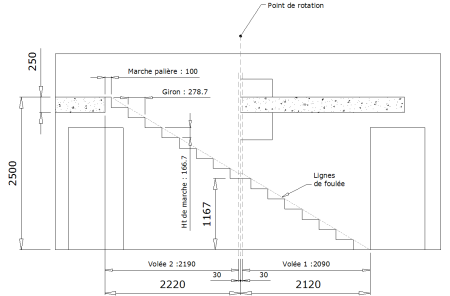
Une fois tracé, voici le résultat :
Il faut également implanter les ouvertures sur cette vue pour pouvoir détecter les interférences et ne pas se retrouver avec un escalier traversant une fenêtre.
On reporte les marches sur la vue en plan de l’escalier droit.
On coupe l’escalier droit au niveau du point de rotation et on replace les deux parties d’abord sur la vue en plan puis sur les vues principales de l’escalier.
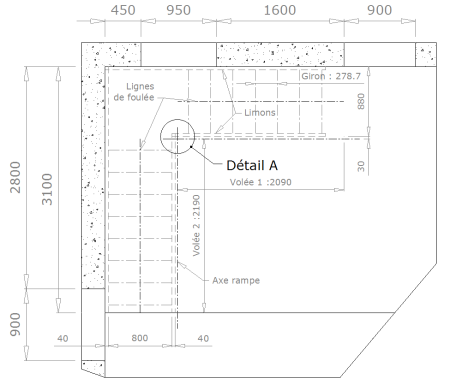
4.1.1.5 - Tracer les limons
La dernière étape, c’est la traçage des limons
La dernière illustration montre bien la qualité du raccord entre les main-courantes. Par contre, même si en générale les limons se raccordent bien, il peut y avoir des défauts s’ils sont très épais ou l’angle de monté très important.
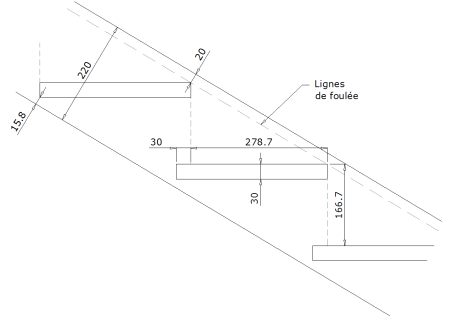
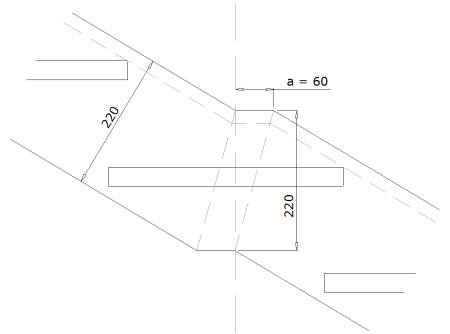
Pour la fabrication, nous allons faire le développé de la face extérieure du limon à partir du plan précédent.
On positionne le point de rotation sur l’intersection des deux faces extérieures des limons.
On trace le développé de l’escalier
On implante les marches et on détermine la largeur du limon
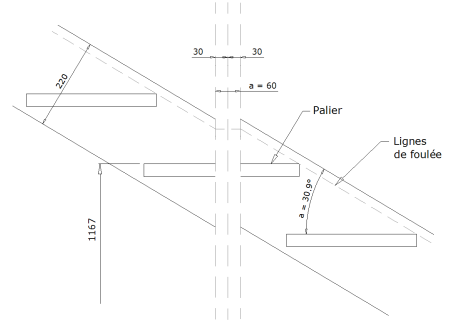
On raccorde les limons au niveau du point de rotation.
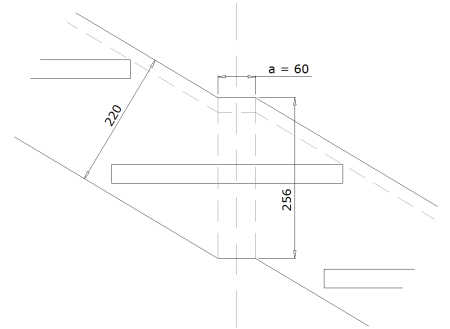
Il existes deux façon de raccorder les limons en fonction de la dimension de a.
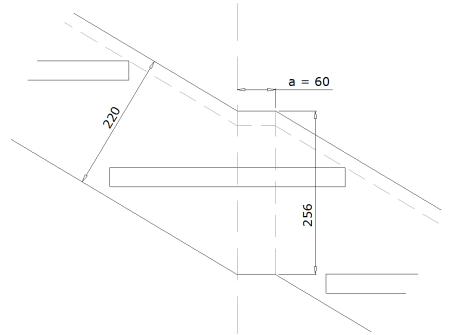
4.1.1.5.1 - Raccord continu
Si :
$a \ge Tan({\frac {Angle De Monte De L Escalier} {2}}) \times Largeur Du Limon$
Ce type de raccord permet de garder une largeur de limon constante et donc préserve l’esthétique de l’escalier.
Quelquefois, il suffit simplement d’éloigner la main courante de quelques centimètres supplémentaires du limon pour pouvoir obtenir ce type de raccord.
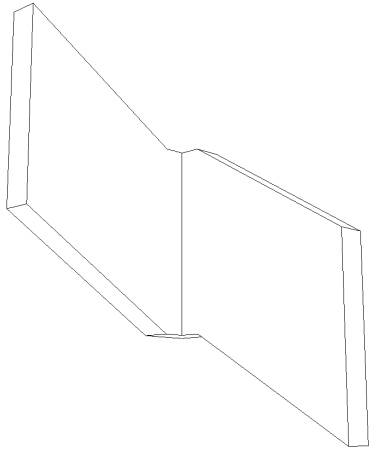
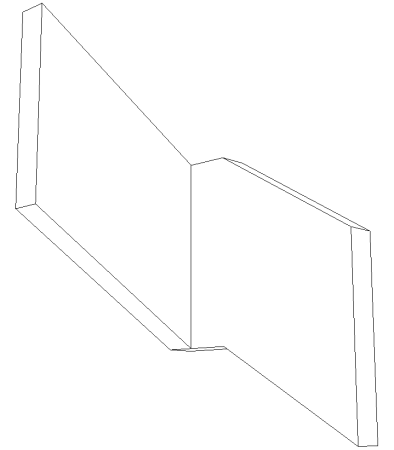
4.1.1.5.2 - Raccord direct
Si :
$a < Tan({\frac {Angle De Monte De L Escalier} {2}}) \times Largeur Du Limon$
Ce type de raccord augmente la hauteur du limon au niveau du palier. Si l’angle de monté de l’escalier est important, cette différence peut être flagrante. Au niveau de la fabrication, ce type de raccord oblige à débiter une portion de limon dans un autre profil plus large. Dans le cas d’un limon en tube rectangulaire, ca peut poser des problèmes puisque toutes le dimensions n’existe pas.
Dans notre cas, $[Tan({\frac {30.9} {2}}) \times 220 = 60.8] \approx a$, les deux solutions sont donc possibles.
Raccord direct :
Le raccord n’est pas obligatoirement centré, cela permet d’économiser un assemblage
Raccord continu :